Crack-inclusion-T-stress interaction

Last updated on Jul 9, 2020

Fracture under crack-inclusion interaction

Particulate composites are widely used in engineering applications and observed in nature, ranging from structural composites, energy storage materials to nacre shells. The interaction between cracks and the second phase particles (i.e., inclusions with different elastic properties) often play key roles in the critical failure of these mateirals systems (Fig 1).

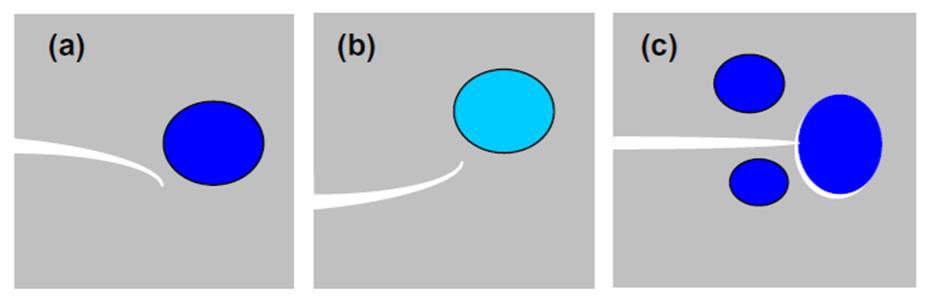
Fig. 1 Fracture behavior under crack-inclusion interaction [1-6]

Correspondly, analytical approaches, numerical simulations as well as advanced experimental observations have long been devoted to understand how cracks interact with inclusions. A widely known conclusion from existing studies is that (Fig 2),

a stiff inclusion tends to repel a approaching crack
a soft inclusion tends to attract a approaching crack
Interfacial debonding tends to start from a stiff inclusion

Fig. 2 A rule of thumb of crack-inclusion interaction [7]

When T-stress comes into play

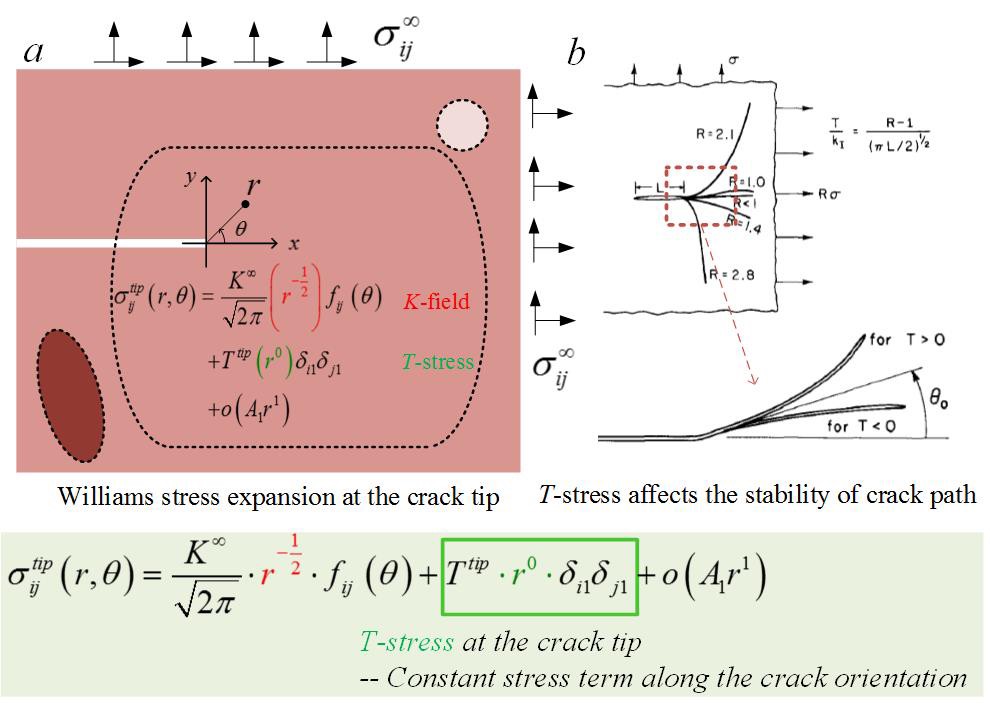
However, one might note that the rule of thumb above has been primarily drawn from the hehavior of the singular stress field near the crack tip, i.e., the K-field. On the ohter hand, it is also known that the constant term in the Williams expansion of the crack tip field, the so-call T-stress which acts in parallel to the crack, can strongly influence the propagation path of a mode I crack. So far, the effect of T-stress on the crack-inclusion interaction has been rarely discussed.

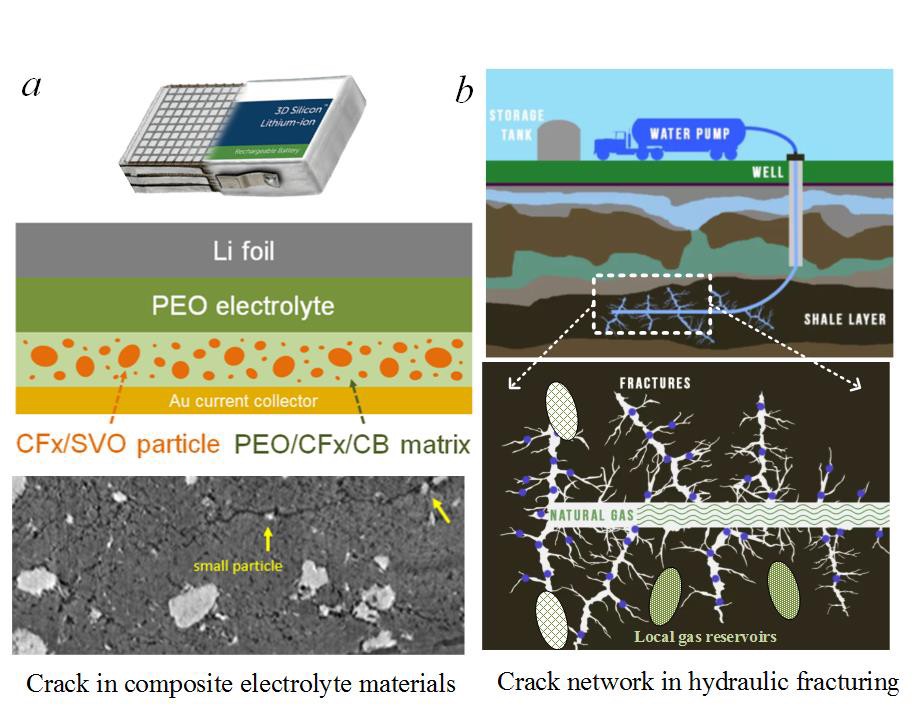
Fig. 3 Interaction between crack and T-stress [8]

At the same time, some advanced application/manipulation of particulate composite systems happen in the presence of a significant compressive T-stress. The interaction between T-stress, inclusion and crack can be critical to the reliability and performance. For instance, composite electrodes in lithium-ion batteries (Fig. 3a) undergo substantial compressive stresses due to Li intercalation into active materials. The attraction between cracks and active material particles can induce capacity fade through loss of contact between the matrix and active materials. In addition, hydraulic fracturing designed for stimulating unconventional reservoirs (e.g., tight gas and shale) has attracted interests from the oil and gas industry in recent years. Underground shales (Fig. 1b) naturally undergo a triaxial compressive loading (Gomez and He 2006; Gramberg 1965), resulting in significant T -stress during the fracturing process. The T -effect on crack-inclusion interaction can play a crucial role in promoting/suppressing crack networks in connecting rock pores which store natural gas, affecting overall gas production.

Fig. 4 Fracture cases under compressive T-stress: composite electrolyte and hydraulic fracturing

A micromechanics analysis

The present work is aimed to investigate the effect of an applied T-stress on the trajectory of a crack in the vicinity of an inclusion. Through an integrated theoretical and numerical approach, we will demonstrate that a sufficiently large compressive applied T-stress can fundamentally change the interaction between cracks and inclusions in particulate composites.

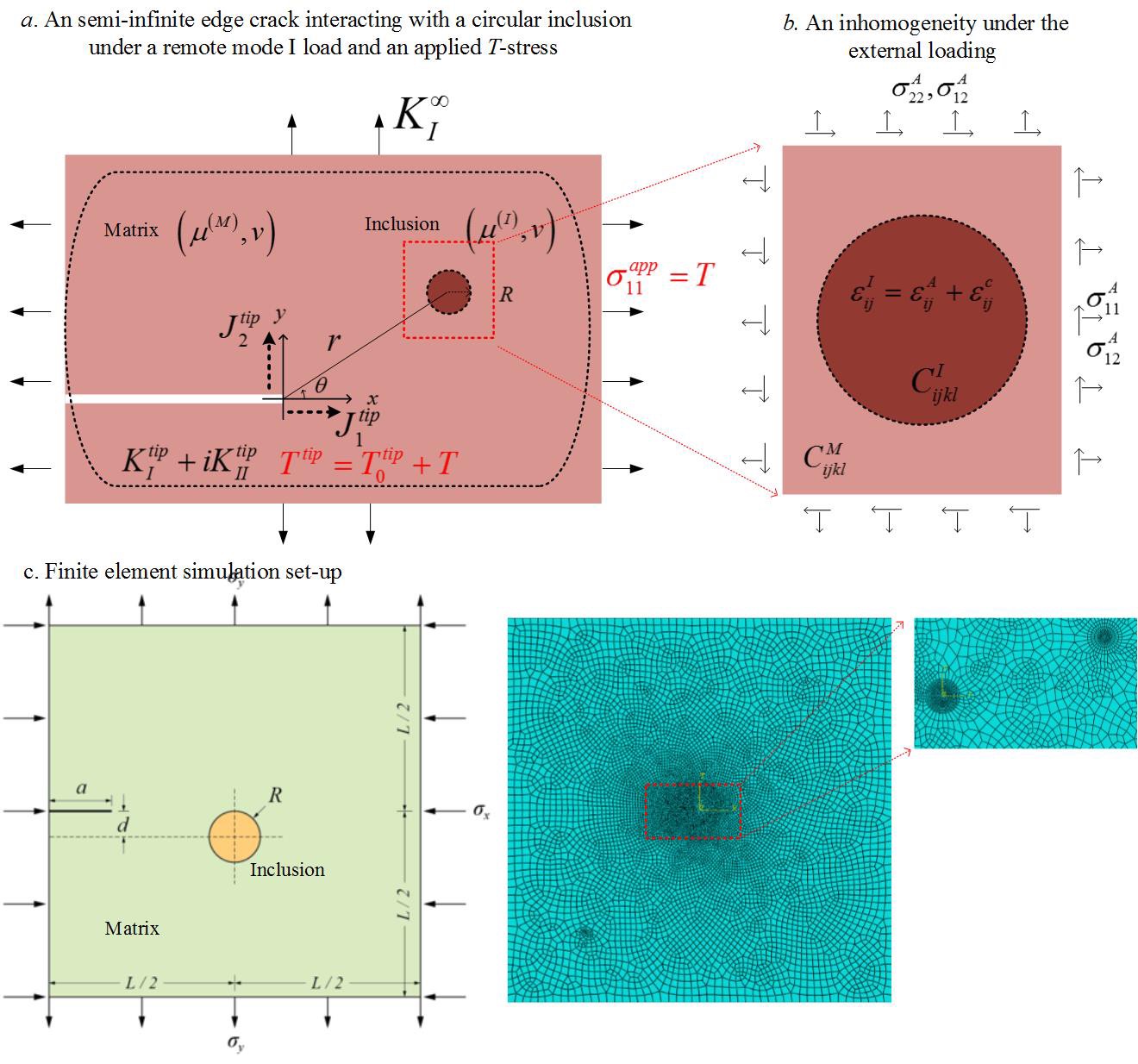
Without the loss of generality, we consider a theoretical model including an edge crack under remote loading, an circular inclusion and an applited T-stress. By solving the elasticity field using Eshelby inclusion theory, we derive the drivigng forces on the inclusion as well as the crack using J-integral. Finite element simulaiton and extended finite element method are used to validate the analytical results.

Fig. 5 The model micromechanics analysis and FEM simulations

The rise of T-stress effect

Fig. 6 The driving force at the crack tip under the presence of an inclusion and an applied T-stress

Based on the analytical model, it is found that only under the presence of the inclusoin, the applied T-stress can have a direct contribution to the driving force on the crack tip. More surpingly, this three-party interacton between crack, inclusion and T-stress (Red in Fig. 6) decays slower than the crack-inclusion (Blue in Fig. 6) interaction. Potentially, the effect of T-stress can compete with, or even overcome the original trend of crack-inclusion interaction.

Conventional or unconventional – crack deflection under applied T-stress

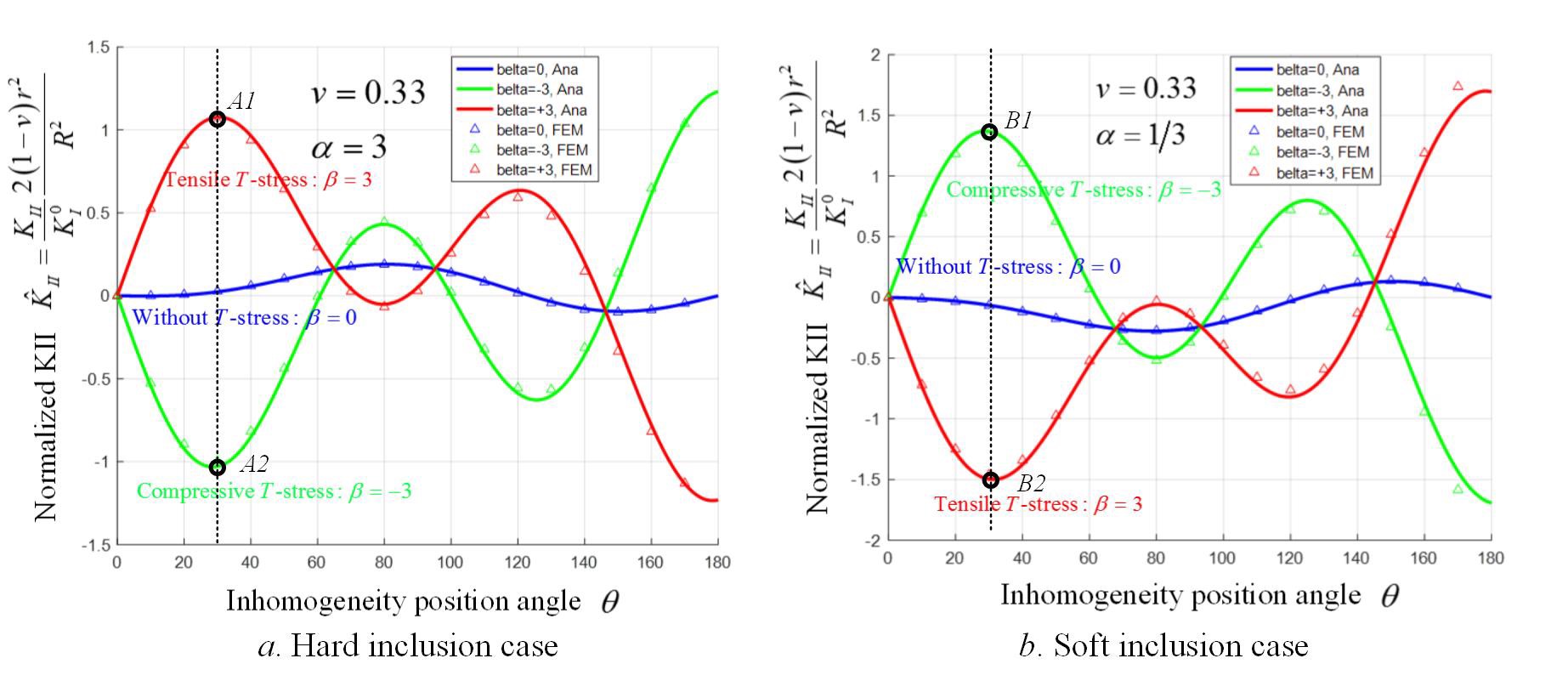
According to fracture mechanics, the mode II stress intensity factor, KII, indicates the deflection of the crack. Here, we derive the normalized KII under the influence of the incluion and the applied T-stress (Fig. 7) and get a good agreement with the results of FEM calculations.

Fig. 7 Mode II SIF at the crack tip under the presence of applied T-stress

Based on Fig. 7, for an crack with an inclusion sitting head of it, we find the following.
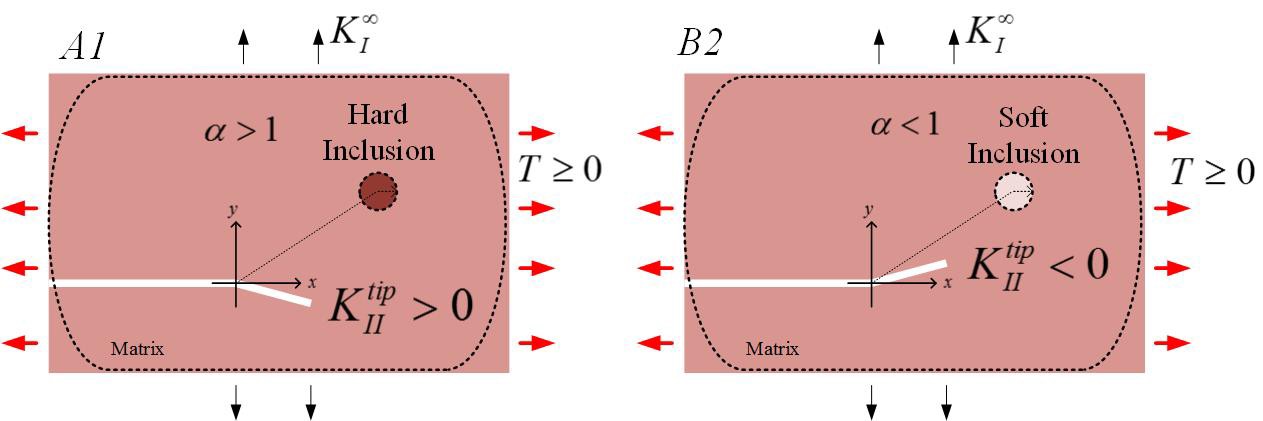
Under a tensile applied T-stress,

Hard/soft inclusion tend to repel/attract the crack
The conventional trend of crack-inclusion interaction is ampified.

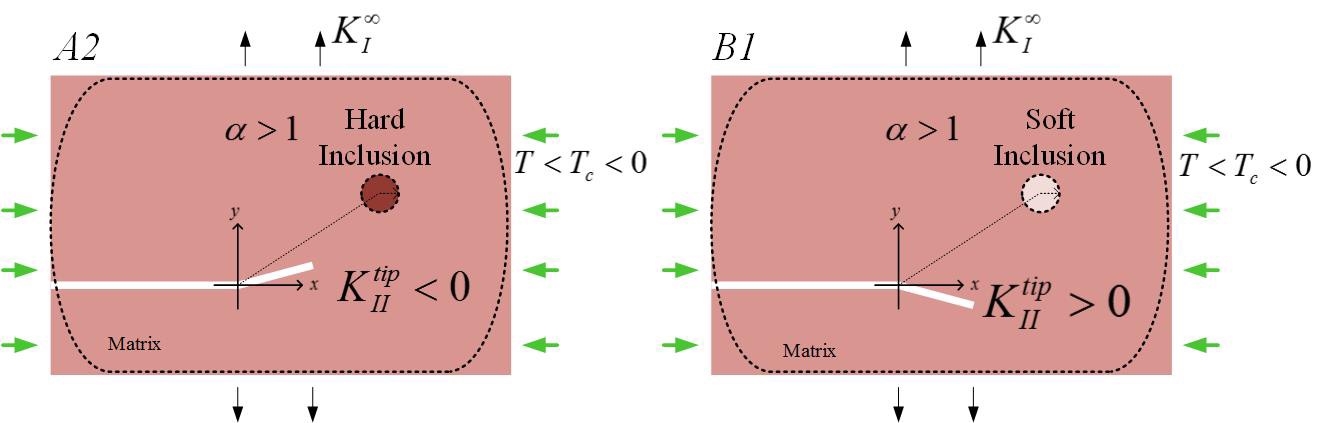
Fig. 8 Amplifiy the conventional trend: crack deflection trend under different combination of inclusion (hard/soft) and an tensile applied T-stress

Under a large enough compressive applied T-stress,

Hard/soft inclusion tends to attract/repel the crack
The conventional trend of crack-inclusion interaction is reversed.

Fig. 9 Reverse the conventional trend: crack deflection trend under different combination of inclusion (hard/soft) and an compressive applied T-stress

T-stress in action: a crack propagtion simulation

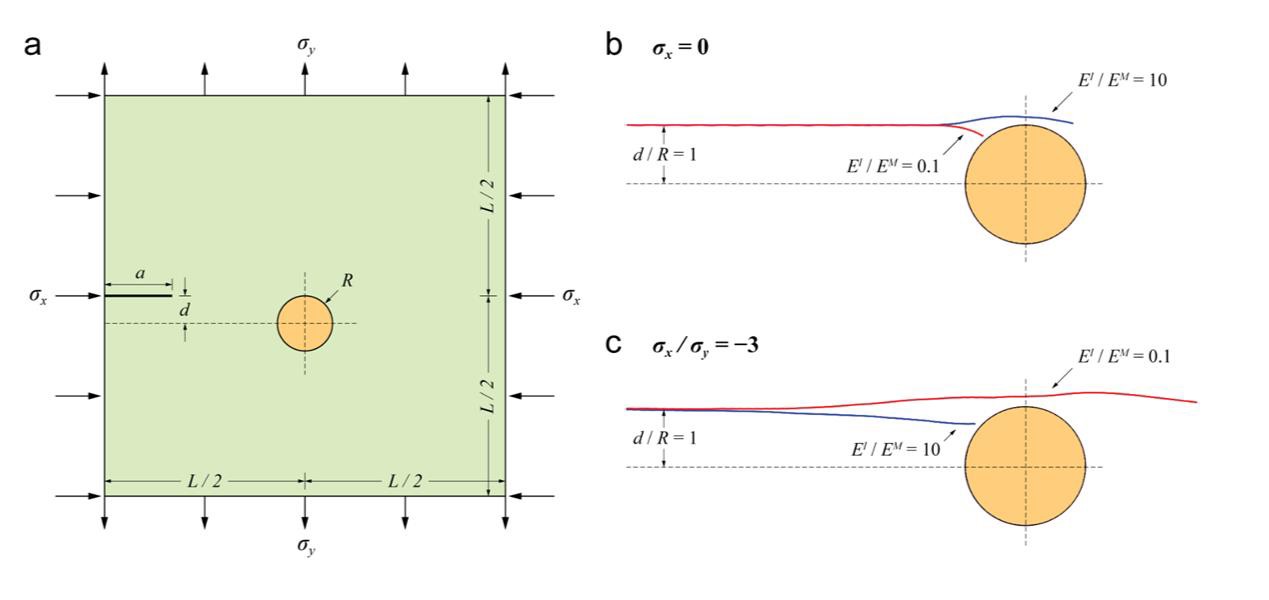
To demonstrate the effect of T-stress on the propagation process of the crack, we adopt XFEM to simulation the crack path. As shown in Fig. 10, as the crack propagates, the detailed interaction can vary. Still, the conventional trend of crack-inclusion can be reversed under a large enough compressive applied T-stress.

Fig. 10 XFEM simulation of crack propagation paths

Take-home message:

Under a tensile applied T-stress, the effect of inclusion on crack tip can be amplified.
Under a strong enough compressive applied T-stress, the effect of inclusion on crack tip can be reversed, i.e., soft inclusion can repel crack while hard inclusion can attract crack.
It explains the failure in some lithiumion batteries. Lithium intercalation into high capacity active materials such as silicon can induce substantial compressive stress in the electrodes. Thus, cracks propagating in the matrix would be attracted towards the stiff active particles, which could further induce capacity fade through the detachment of the activematerial particles from the conductive matrix.
Applied T-stress provides an novel way to tune crack-inclusion interaction in composite materials and systems.
For instance, high compressive T -stress for hydraulic fractures might cause repulsion between the pores and induced cracks. Due to the gravity effect, underground shales undergo a triaxial differential compressive loading and the major compressive principle stress is usually along the vertical direction, so horizontal hydraulic fractures are likely to provide higher gas production by passing through more rock pores in comparison with vertical fractures.

More detailes can be found in the following publication.

Guo K*, Ni B*, Gao H. Tuning crack-inclusion interaction with an applied T-stress. International Journal of Fracture. 2020 Feb 3:1-1. (* contributed equally)

References:

R. O. Ritchie, Acta Materialia 148, 147 (2018).
I. Sevostianov, V. Levin, and E. Radi, International Journal of Engineering Science 100, 61 (2016).
N. Chawla and V. Ganesh, International Journal of Fatigue 32, 856 (2010).
U. G. Wegst, H. Bai, E. Saiz, A. P. Tomsia, and R. O. Ritchie, Nature materials 14, 23 (2015).
J. Song, C. Fan, H. Ma, L. Liang, and Y. Wei, Acta Mechanica Sinica 34, 143 (2018).
M. Ambati, T. Gerasimov, and L. De Lorenzis, Computational Mechanics 55, 383 (2015).
R. Zhou, Z. Li, and J. Sun, Composites Part B: Engineering 42, 1999 (2011).
B. Cotterell and J. Rice, International journal of fracture 16, 155 (1980).

PhD student

I’m a solid mechanics researcher who loves learning new tools and solving coupling problems.