Deep learning approch to inverse problems in elastograhy

Abstract

Non-destructive evaluation (NDE) of elastic modulus in materials has broad applications in fields such as geological exploration, quality evaluation and medical diagnosis. A key to these techniques is to solve the inverse problem of identifying the distribution of elastic modulus. While conventional theories and numerical methods often involve solving multiple variational problems iteratively for each individual case, the demand of real-time response and high-throughput application of NDE is growing, especially for advanced manufacturing and clinical practices.

To address this challenge, in this letter, we leverage some of the recent progress in data science and propose a deep learning (DL) approach to solve the inverse problem of modulus identification in elasticity. By designing the sampling spaces of smooth distribution of shear modulus and adopting a conditional generative adversarial network (cGAN), we demonstrate that the DL approach can learn the high-dimensional mapping between distributions of strain and shear modulus via training over a limited portion of data. Also, the model can be rapidly deployed with high accuracy, bypassing the iterative solving process in the conventional methods. This work broadens the way of solving challenging inverse problems that aim for applications in real-time elastography and high-throughput NDE techniques.

Inverse problem – the key to NDE

Due to their non-invasive nature, non-destructive evaluation (NDE) techniques for identifying elastic modulus distribution in materials have attracted increasing attention in various fields, ranging from geological exploration, construction quality control, composite material evaluation, to medical diagnosis. A common core of these techniques is to solve inverse problems in elasticity. For example, elastography aiming at distinguishing tissues based on a quantitative distribution of elastic modulus has gained broad applications in breast tumor characterization and hepatic fibrosis staging.

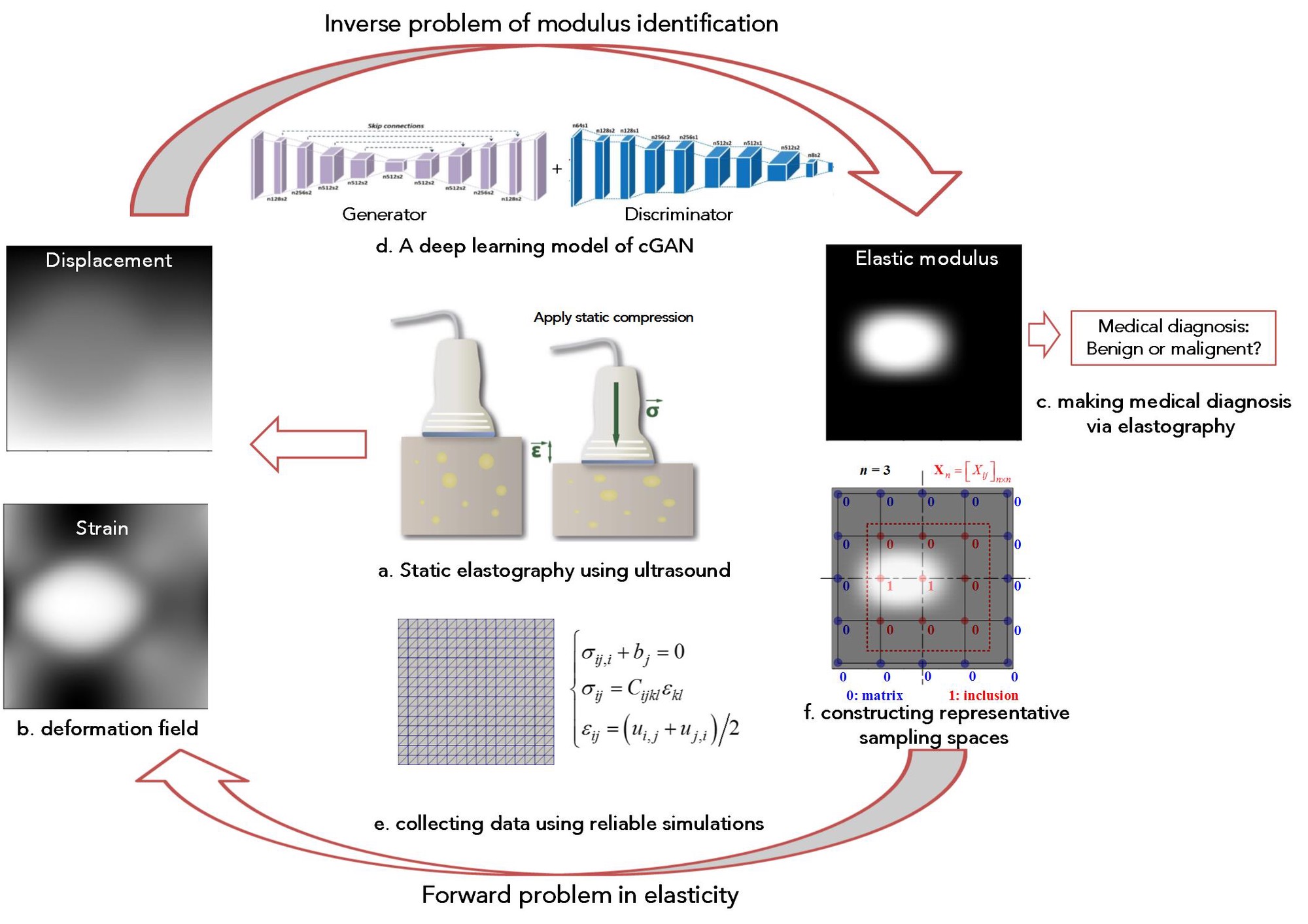
During a quasi-static ultrasound elastography, external compression is applied to the tissue of interest and the deformation fields are estimated using two-dimensional (2D) correlation of ultrasound images (Figure 1a and 1b). To identify the abnormal tissues based on elastic heterogeneity (Figure 1c), an inverse problem of reconstructing the distribution of elastic modulus based on the displacement/strain images needs to be addressed. Thus, solving such inverse problems plays key roles in successful applications of elastography. (Fig 1).

The challenge of solving inverse problems

Generally speaking, solving inverse problems of elasticity accurately and efficiently can be challenging, especially when real-time response (10) and high-throughput applications (11) are in demand.

• Comparing to the forward problem (i.e., to obtain the deformation field under given elastic properties), the inverse problem is more expensive to solve.

For example, in the adjoint-weighted approach, solving inverse problem is treated as an constraint optimization process and multiple variational problems have to be solved iteratively.

• There is growing demand in solving inverse problems for real-time response and high-throughput applicatoins.

For instance, tissue elastography in real time shows promising applications in diagnosing breast, prostate, thyroid and pancreatic diseases, even in hope to substitute biopsy (15). Ultrasound based NDE techniques have proven potentials in high-throughput screening and fabrication of laser additive manufactured metallic glasses (11).

• Not to mention the issues of noised data, nonlinearity and ill-posedness for various inverse problems.

A new hope from deep learning

Recent progresses in machine learning (ML) provide a new angle to address this challenge. ML, especially deep learning (DL), has proven capable of learning hidden relations between complex patterns from large amount of data, including image classification, replacing interatomic potential in MD as well as predicting crack pathes. The advanced learning capability and accessibility to representative data make DL models promising candidates to tackle the inverse problem in elasticity.

• Deep learn models such as conditional generative adversarial networks (cGAN) have demonstrated strong learning capabilities and can handle mapping between images.
• Affordable accesses exist to collect reliable date in elasticity problems (finite element method for example).

It should be noted that DL models have already been applied to improve the performance of medical imaging including elastography. However, most of these developments deal with end-to-end applications while the middle step of solving the inverse problem of elasticity is often circumvented (26)

In the present work, we focus on the inverse problem of identifying modulus distribution in elasticity itself and propose a DL approach to address this fundamental problem in elasticity. By designing representative sampling spaces for smooth distribution of shear modulus (Figure 1f) and constructing a cGAN model (Figure 1d), we demonstrated that the proposed DL approach can learn the high-dimensional mapping between distributions of strain and shear modulus via training over a limited portion of data and achieve high efficiency and accuracy at deployment.

Building representative sampling spaces

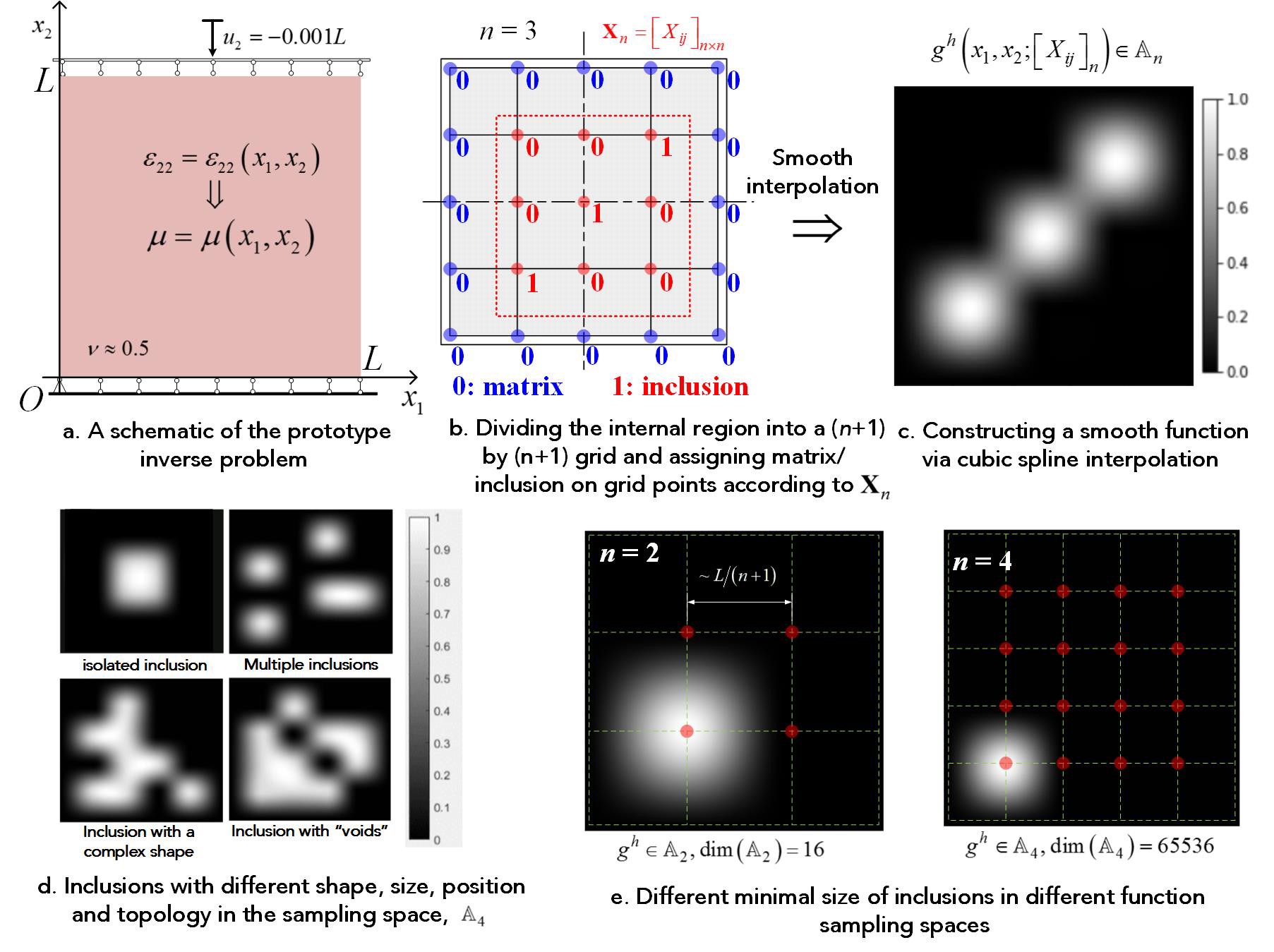
Collecting relevant and representative data often plays a key role in a data-driven approach. Here, we consider the set-up of a static elastography test (Figure 2a) and construct a prototype problem of matrix-inclusion distributions. By descretizing the domian of interest (Figure 2b and 2c), we construct a series of finite function spaces, An, n = 2,3,4,…, to describe the possible distribution of shear modulus of a incompressible issue, in which the number, shape, size and topology of inclusions can vary (Figure 2d). And as n increases, the minimal dimension of the inclusions decreases (Figure 2e). Since the region of interest in elastography is often finite and only inclusions with a detectable size are of concern, in the following we focus on the cases of a finite n.

Over the sampling spaces, An, we use finite element method to solve the forward problem of elasticity and collect the relative distributions of shear modulus and strain images as the training data for the deep learning model.

A cGAN model and its magic

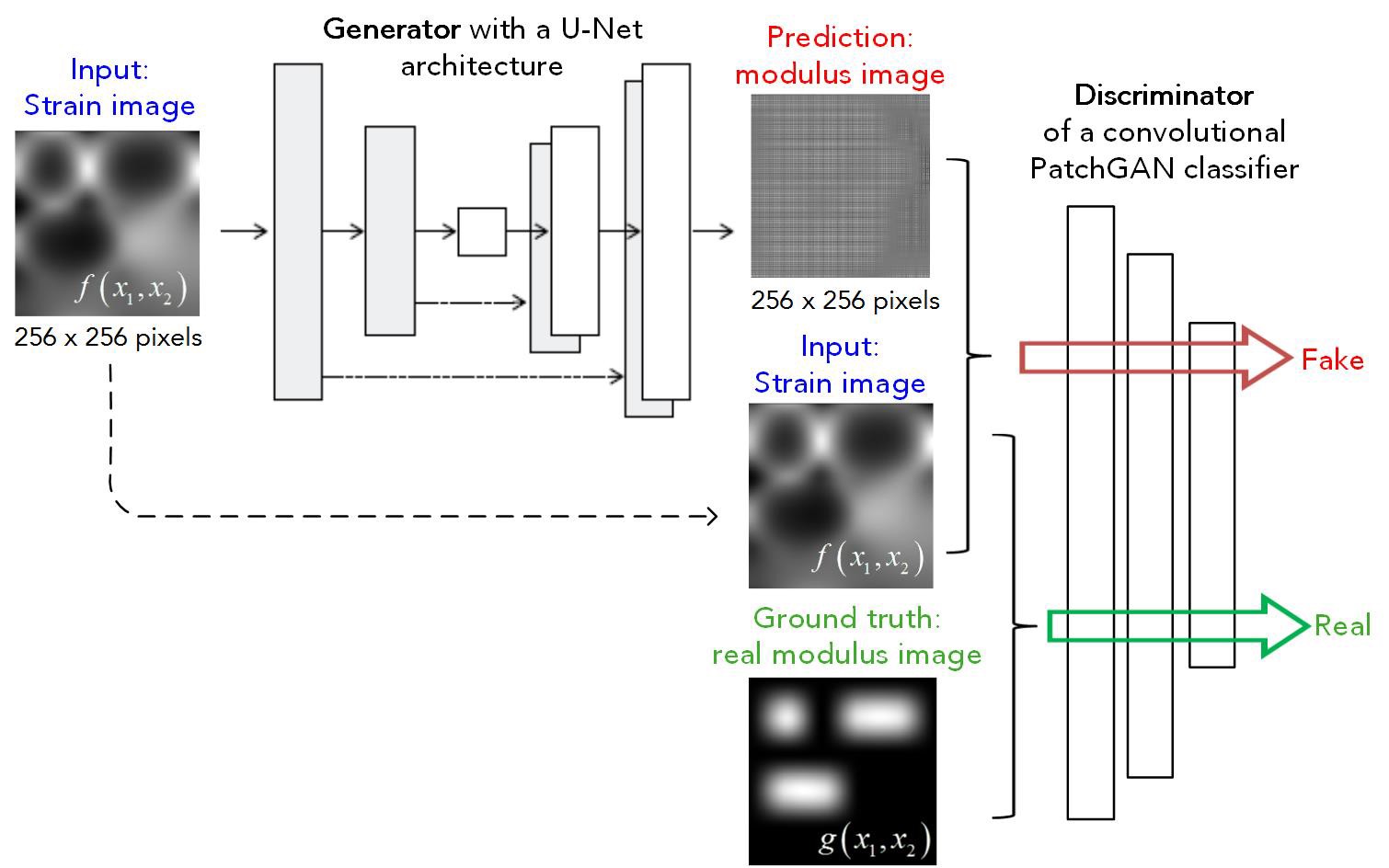
We leverage the recent development of image-to-image translation in ML study and construct a cGAN model to learn the mapping between images of strain and shear modulus.

The cGAN model consists of a U-Net architectured generator and a convolutional “PatchGAN” classifier(Figure 3), which have proven useful in various image-to-image tasks (22, 23). Here, the generator aims at creating suitable modulus images conditioned by the input of strain images while the discriminator learns to identify the “fake” modulus images created by the generator from the real ones. Through training, the performance of the two improves adversarially until reaching a Nash equilibrium (29), i.e., the generator creates modulus images so real that the trained discriminator cannot distinguish them from the real ones. Beside this adversarial objective, minimizing loss of the prediction is also mixed in the training objective for better performance, as suggested in previous studies (30).

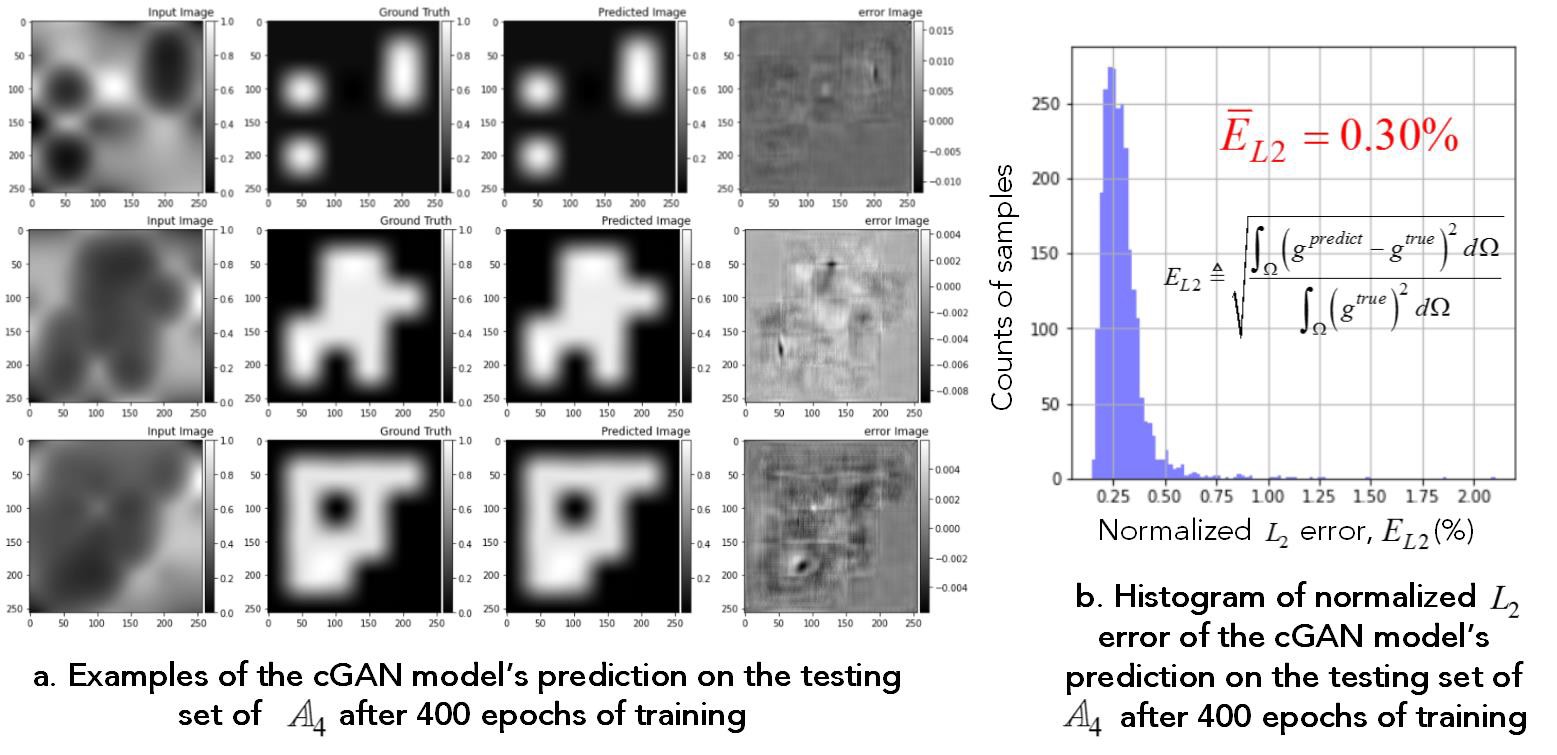
The performance of the cGAN model is tested over the cases in A4. After trained over the training set (70% of total samples) for 400 epochs, the cGAN model can

• make accurate predictions in the testing set (15% samples), which it has never seen before.

For example, three randomly picked examples are shown in Figure 4a and the predicted distributions agree well with the ground truth. On average, a normalized L2 error of 0.30% is achieved in the testing set (Figure 4b).

• The well trained cGAN model is also efficient at deployment, as only the generator in the cGAN model is activated when applied to the testing set.

Making prediction for one input takes about 0.06 second in a freely accessed Google Codelabs platform. The iterative steps of solving multiple variational problems in the conventional methods for the inverse problem in elasticity, which can take minutes (13), is bypassed for all testing cases in the sampling space. This time-efficiency at deployment makes it promising for applications requiring real-time response.

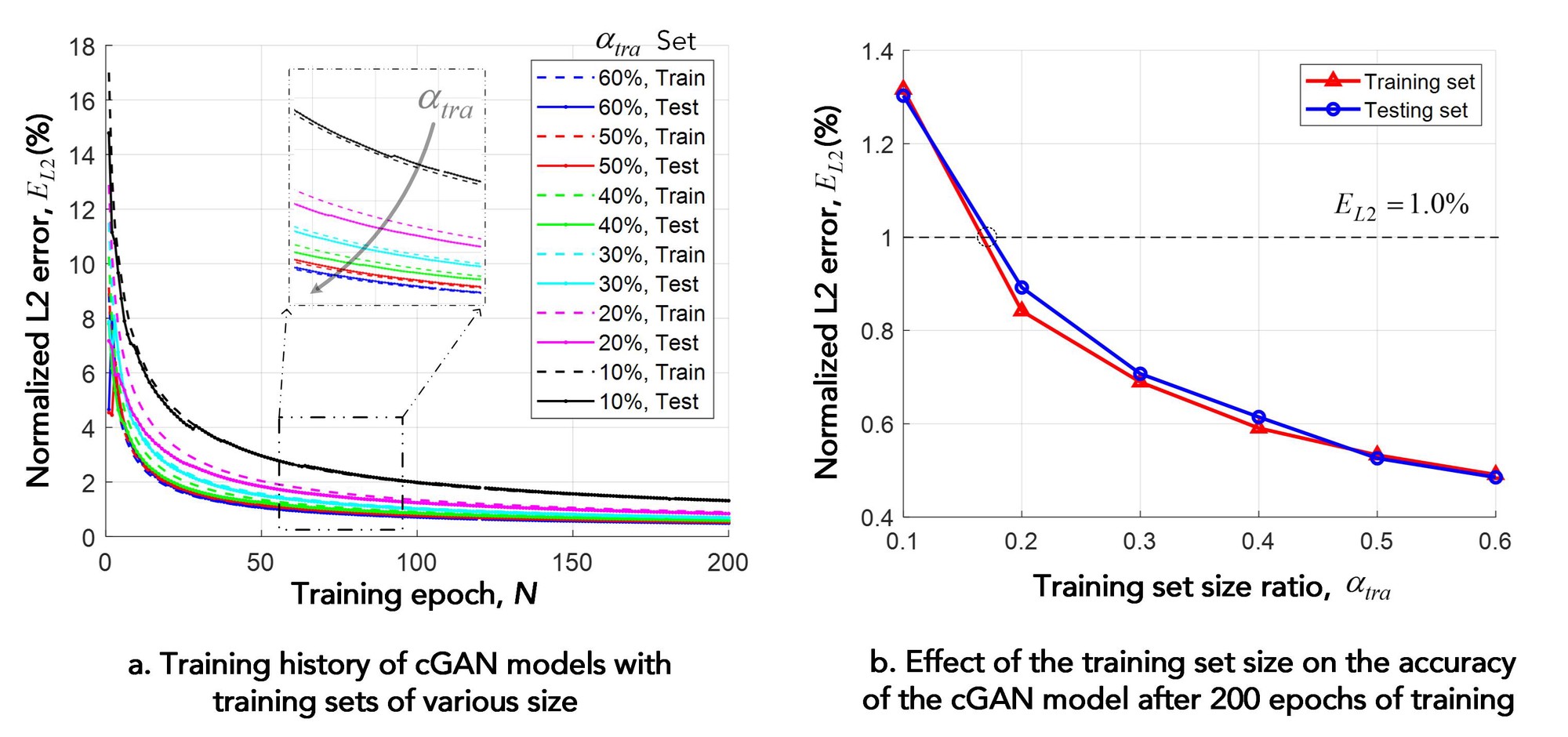
As a data-driven approach, the DL model learns to solve all cases in the sampling space together through training over a limited portion of the data. To demonstrate this generalized predicting capability, we study the effect of the training set size on the performance of the cGAN model over the designed sampling space. For meaningful applications in elastography tests, here we set an accuracy higher than 99% in the L2 sense (the black dash line in Figure 5b) as the goal. Benefited from the representativeness of the designed sampling space and the learning capability of the cGAN model, we find training over a 20% portion of the samples for 200 epochs is enough to fulfill this goal and make predictions with a L2 error less than 1% for the remaining 80% samples in A4, which the cGAN model has never seen before.

• This effectiveness of a finite size of the training set further reduces the training cost of the DL model for a targeted accuracy and demonstrate the efficiency of the DL approach in learning the underlying mapping between strain and shear modulus in the designed sampling space.

This learning efficiency may open doors to high-throughput applications in NDEs.

Conclusion and outlook

In this study, we leverage some of the recent progresses in ML to address the inverse problem of modulus identification in elasticity that involves matrix-inclusion systems mimicking an elastography set-up. By designing representative sampling spaces and constructing capable cGAN models, we demonstrated that the DL approach can efficiently learn the high-dimensional mapping between distributions of strain and shear modulus via training over a limited portion of the samples in the relevant sampling space. At deployment, this approach can response rapidly with high accuracy, bypassing the iterative steps of solving multiple variational problems in the conventional methods.

The DL approach broadens the way of addressing challenging inverse problems in real-time elastography and high-throughput NDE applications. Future studies can further build on this and explore the capability of DL-based approaches in handling challenges such as noised data, nonlinearity and ill-posedness for various inverse problems (31) in fundamental sciences as well as engineering applications.

More detailes can be found in the following publication.

Ni B, Gao H. A deep learning approach to the inverse problem of modulus identification in elasticity. MRS bulletin.(Under review)

References:

1. M. Rodríguez-Sastre, L. Calleja, The determination of elastic modulus of slates from ultrasonic velocity measurements. The Geological Society of London. IAEG 775, 1-11 (2006).
2. E. Martinho, A. Dionísio, Main geophysical techniques used for non-destructive evaluation in cultural built heritage: a review. Journal of Geophysics and Engineering 11, 053001 (2014).
3. E. Reufi, I. Thomas, Evaluation of modulus of elasticity by non-destructive method of hybrid fiber reinforced concrete. Int. J. Adv. Chem. Eng. Biol. Sci. 3, 1-4 (2016).
4. P. Icenogle, S. Kabir, “Evaluation of non-destructive technologies for construction quality control of HMA and PCC pavements in Louisiana,” (Louisiana. Dept. of Transportation and Development, 2013).
5. M. Jalili, A. Pirayeshfar, S. Mousavi, in 29th Eur Conf Aco Emi Test (EWGAE), Vienna, Austria. (2010).
6. S. Gholizadeh, A review of non-destructive testing methods of composite materials. Procedia Structural Integrity 1, 50-57 (2016).
7. J.-L. Gennisson, T. Deffieux, M. Fink, M. Tanter, Ultrasound elastography: principles and techniques. Diagnostic and interventional imaging 94, 487-495 (2013).
8. J. Bercoff et al., In vivo breast tumor detection using transient elastography. Ultrasound in medicine & biology 29, 1387-1396 (2003).
9. R. M. Sigrist, J. Liau, A. El Kaffas, M. C. Chammas, J. K. Willmann, Ultrasound elastography: review of techniques and clinical applications. Theranostics 7, 1303 (2017).
10. H. Hong et al., Performance of real-time elastography for the staging of hepatic fibrosis: a meta-analysis. PloS one 9, (2014).
11. L. Zhai, Y. Lu, X. Zhao, L. Wang, X. Lu, High-throughput screening of laser additive manufactured metallic glass via ultrasonic wave. Scientific reports 9, 1-6 (2019).
12. E. Crossen, M. S. Gockenbach, B. Jadamba, A. A. Khan, B. Winkler, An equation error approach for the elasticity imaging inverse problem for predicting tumor location. Computers & Mathematics with Applications 67, 122-135 (2014).
13. A. A. Oberai, N. H. Gokhale, G. R. Feijóo, Solution of inverse problems in elasticity imaging using the adjoint method. Inverse problems 19, 297 (2003).
14. N. H. Gokhale, P. E. Barbone, A. A. Oberai, Solution of the nonlinear elasticity imaging inverse problem: the compressible case. Inverse Problems 24, 045010 (2008).
15. L. Feril, Can Ultrasound Elastography Substitute Tissue Biopsy in the Diagnosis of Malignancy. MJ Cancer 1, 004 (2016).
16. A. Krizhevsky, I. Sutskever, G. E. Hinton, in Advances in neural information processing systems. (2012), pp. 1097-1105.
17. F. Brockherde et al., Bypassing the Kohn-Sham equations with machine learning. Nature communications 8, 1-10 (2017).
18. H. Wang, L. Zhang, J. Han, E. Weinan, DeePMD-kit: A deep learning package for many-body potential energy representation and molecular dynamics. Computer Physics Communications 228, 178-184 (2018).
19. D. Z. Huang, K. Xu, C. Farhat, E. Darve, Learning constitutive relations from indirect observations using deep neural networks. Journal of Computational Physics, 109491 (2020).
20. Y.-C. Hsu, C.-H. Yu, M. J. Buehler, Using Deep Learning to Predict Fracture Patterns in Crystalline Solids. Matter, (2020).
21. X. Yi, E. Walia, P. Babyn, Generative adversarial network in medical imaging: A review. Medical image analysis, 101552 (2019).
22. M. Mirza, S. Osindero, Conditional generative adversarial nets. arXiv preprint arXiv:1411.1784, (2014).
23. P. Isola, J.-Y. Zhu, T. Zhou, A. A. Efros, in Proceedings of the IEEE conference on computer vision and pattern recognition. (2017), pp. 1125-1134.
24. A. F. Bower, Applied mechanics of solids. (CRC press, 2009).
25. S. Wu et al., in International Conference on Medical Image Computing and Computer-Assisted Intervention. (Springer, 2018), pp. 374-382.
26. D. Patel et al., Circumventing the solution of inverse problems in mechanics through deep learning: Application to elasticity imaging. Computer Methods in Applied Mechanics and Engineering 353, 448-466 (2019).
27. P. E. Barbone, J. C. Bamber, Quantitative elasticity imaging: what can and cannot be inferred from strain images. Physics in Medicine & Biology 47, 2147 (2002).
28. P. Wellman, R. D. Howe, E. Dalton, K. A. Kern, Breast tissue stiffness in compression is correlated to histological diagnosis. Harvard BioRobotics Laboratory Technical Report, 1-15 (1999).
29. F. Farnia, A. Ozdaglar, GANs May Have No Nash Equilibria. arXiv preprint arXiv:2002.09124, (2020).
30. D. Pathak, P. Krahenbuhl, J. Donahue, T. Darrell, A. A. Efros, in Proceedings of the IEEE conference on computer vision and pattern recognition. (2016), pp. 2536-2544.
31. M. Bonnet, A. Constantinescu, Inverse problems in elasticity. Inverse problems 21, R1 (2005).
32. M. Abadi et al., in 12th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 16). (2016), pp. 265-283.
33. D. P. Kingma, J. Ba, Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, (2014).