Fracture under interlayer sliding in multilayered 2D materials
Interlayer sliding in multilayered 2D materials
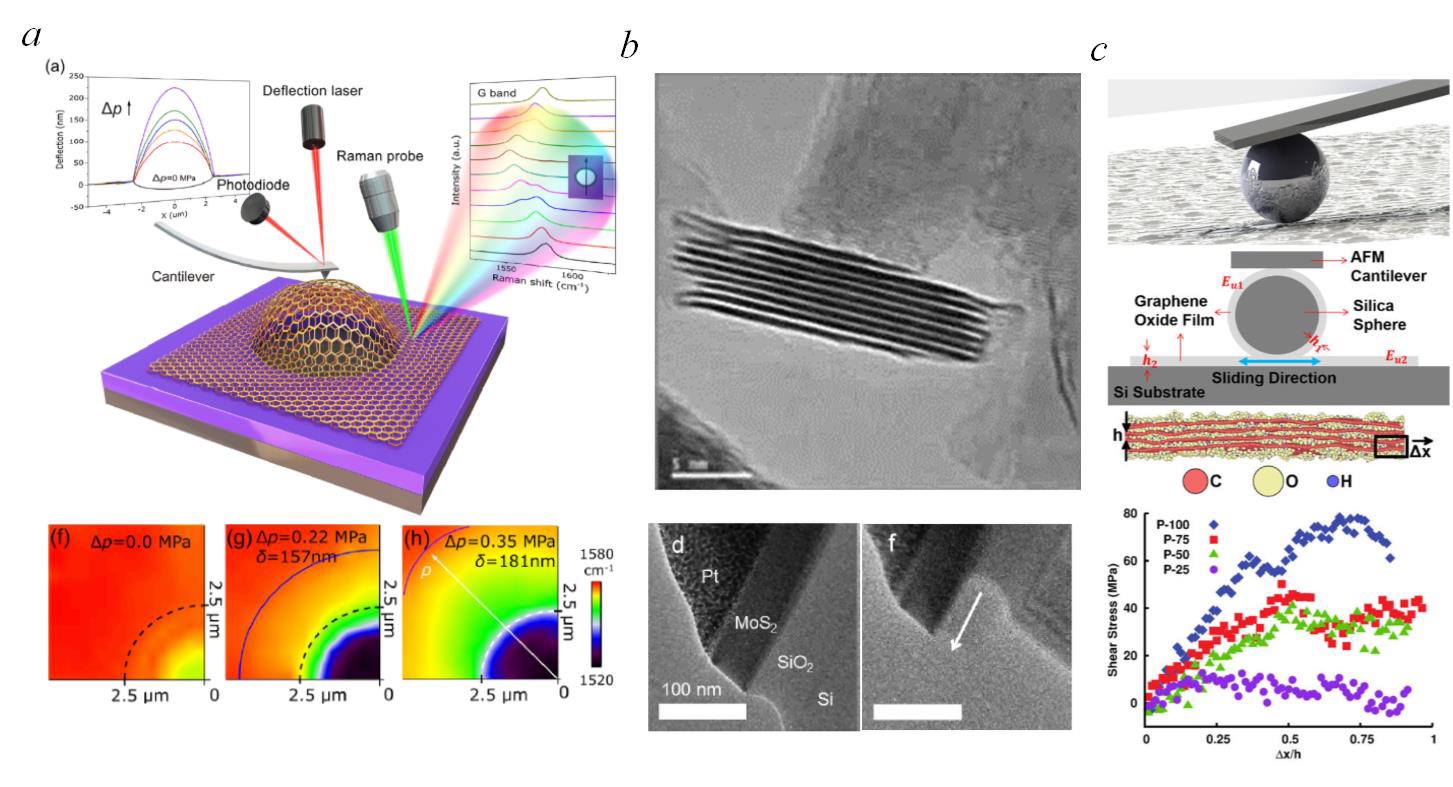
As atomically thin layers, 2D materials have large area of surfaces and interact with surroundings, including other layers, substrate or matrix materials, via interfaces. Consistent efforts have been devoted into understanding the interlayer properties of multilayered 2D materials. For example, different experimental methods have been developed to measure the interlayer shear strength or interlayer sliding stress for 2D materials, including graphene, MoS2, h-BN and graphene oxide films.
Low friction vs low fracture toughness
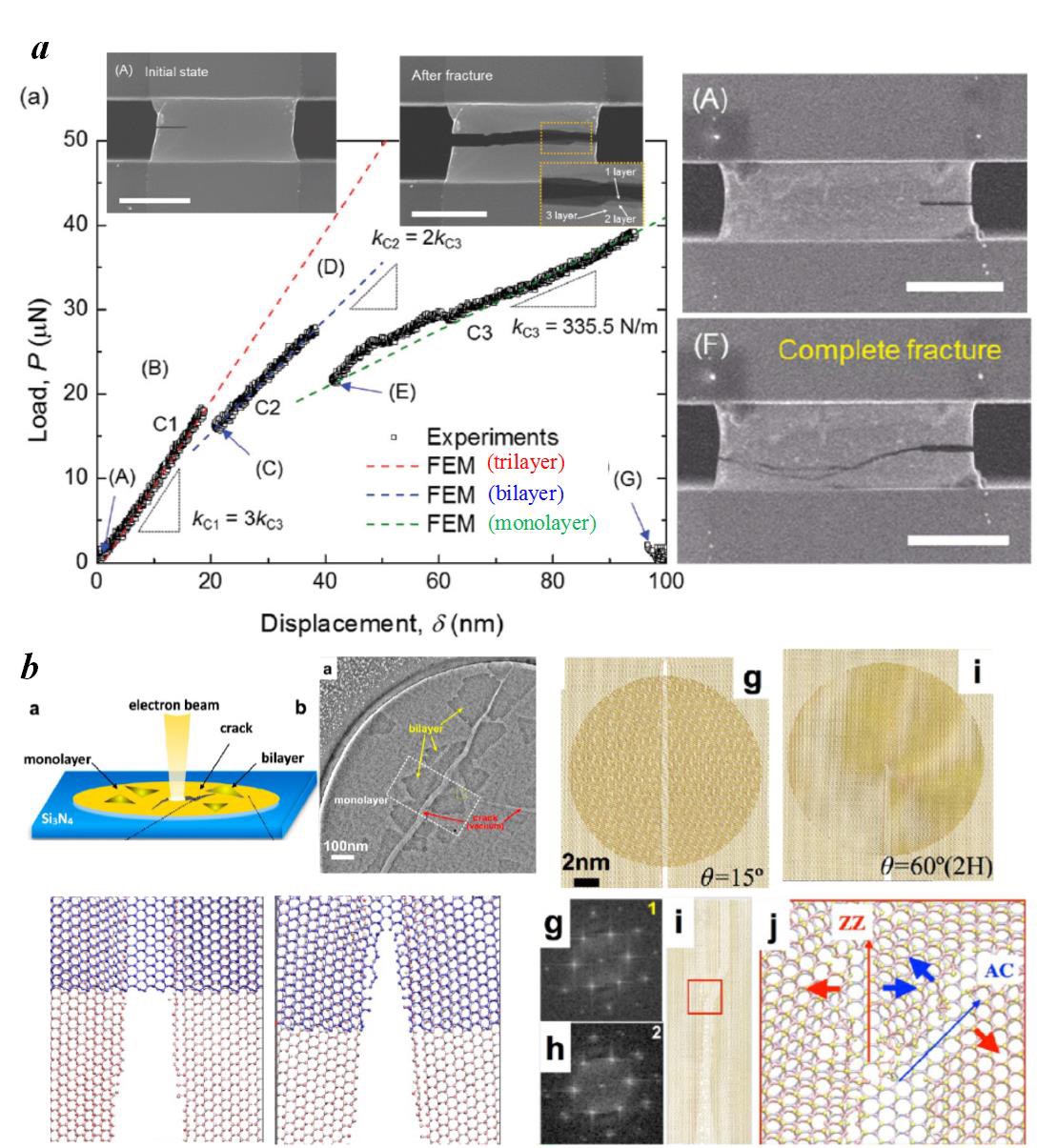
Crystalline 2D materials often show relatively low friction as some of them are good solid lubriant. One contributing factor is the sharp constract between weak interlayer interaction and strong intralayer covalent bonding. At the same time, most 2D materials have low fracture toughness and are fragile to cracks. The coupling between interlayer friction and intralayer fracture remains a possibility. For example, carcks in a trilayered graphene sample is observed to propogate along dissimilar paths in an asynchronous manner. Crack blocking, the second layer fracture and crack branching are captured in bilayered MoS2 via experimental observation and atomistic simulations.
As the application of multilayered 2D materials keeps increasing, ranging from reinforcing phase in composites, protective coating, Van der Waals heterostructures to flexible electronic devices, a systematic understanding of the interaction between interlayer friction and intralyer fracture of multplayered 2D materials gain importances for not only advancing fundamental knowledge in fracture mechanics but also robust engineering performances.
In this study, we focus on the fundamentals of the interaction between interlayer friction and intralayer fracture and propose model problems of asynchronous crack propogation and dissimilar crack paths in the framework combining fracture mechanics and interface mechanics, in hope to unviel the universal feature of the effect of interlayer sliding on cracks in multilayered 2D materials.
Model problems: asynchronous crack propogation and dissimilar crack paths
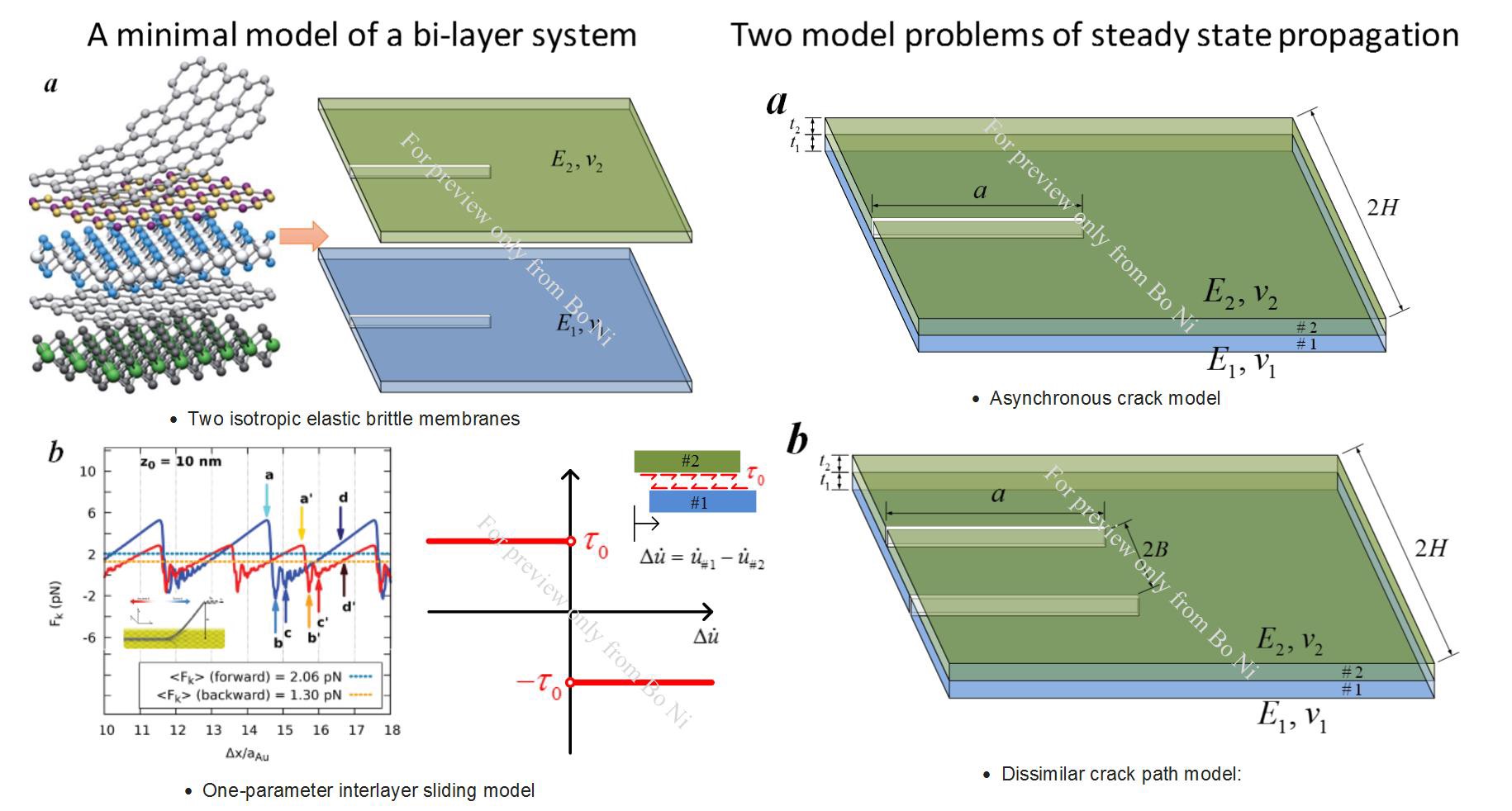
Without the loss of generality, we construct model problems of a bilayered system of brittle elastic membranes. The interlayer shearing stress due to sliding is represented by a constant interlayer sliding strength, tau_0. As the possible geometery of cracks in the two layer can be quite complicated, we focus on two model problems describing the asynchronous crack propogation in time and the dissimilar crack paths in space.
- Asynchronous crack model: an edge crack sitting in the top layer while the bottom layer is intact.
- Dissimilar crack path model: Two parallel edge cracks in two layers respectively.
Via steady steady analysis, we obtain the driving froce on the crack tip and the critical loading for the failure of the bi-layer system. Cohesive element simulations are used to validate the theoretical prediction while phase field modelling is adopted to demonstrate the potential complexity of crack propagation.
As the work is still under development, only some selected results are previewed in the following.
Smaller is stronger, Stiffer is better
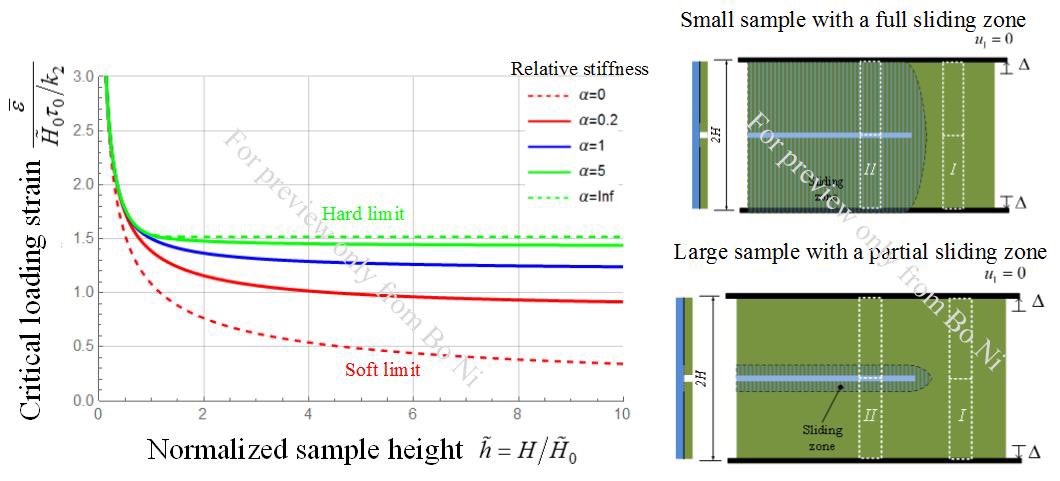
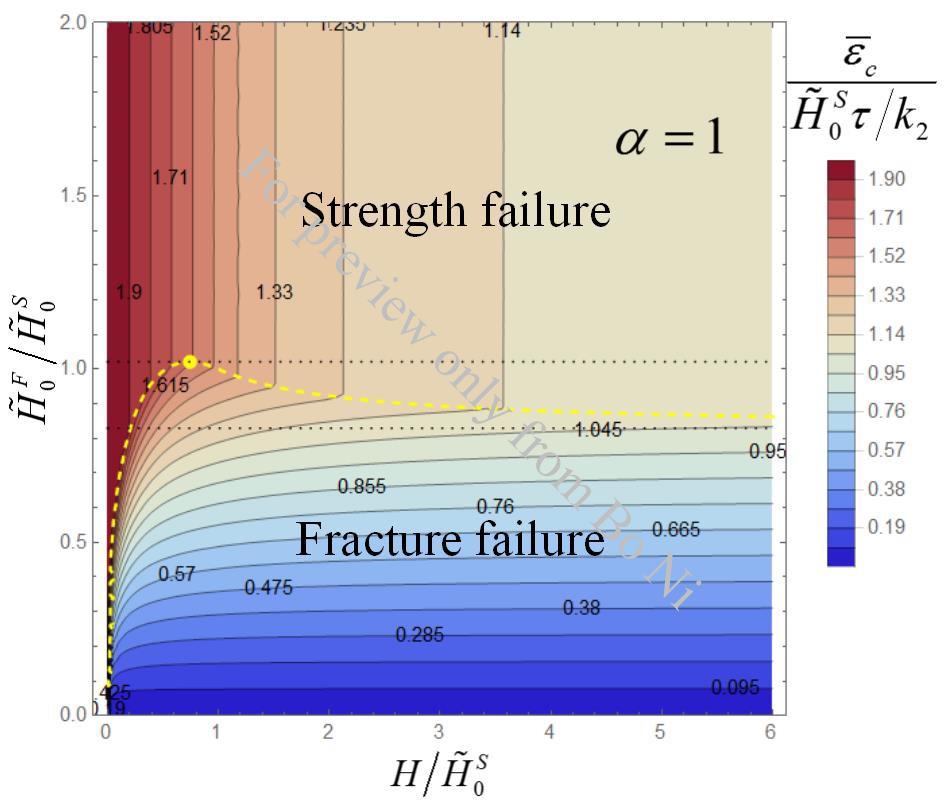
According the theoretical analysis, we find the critical load for the leading crack in the asynchronous crack model to propagate depends on not only the size of the sample but also the stiffness of the bottom layer. As the sample height increases, the critial loading strain will approach to a constant, which is very different from the case of crack propogation in a single layer. Also, choosing a stiff bottom lay can postpone the crack propogation in the top layer and toughen the system.
Leading crack propogation vs second layer failure
For the asynchronous crack model, a competition exists between crack propogation in the top layer and the strength failure of the bottom layer as the two layers can “communicate” via the interlayer friction. By controlling the sample size and the fracture toughness of the material, the failure mode can switch between the two. We draw the phase diagram of this competition and find the good agreement with the numerical simulations.
Crack propogation in the top layer wins.
Strength failure in the bottom layer wins.
Phase diagram of the failure mode
Leading crack propogation vs second layer failure
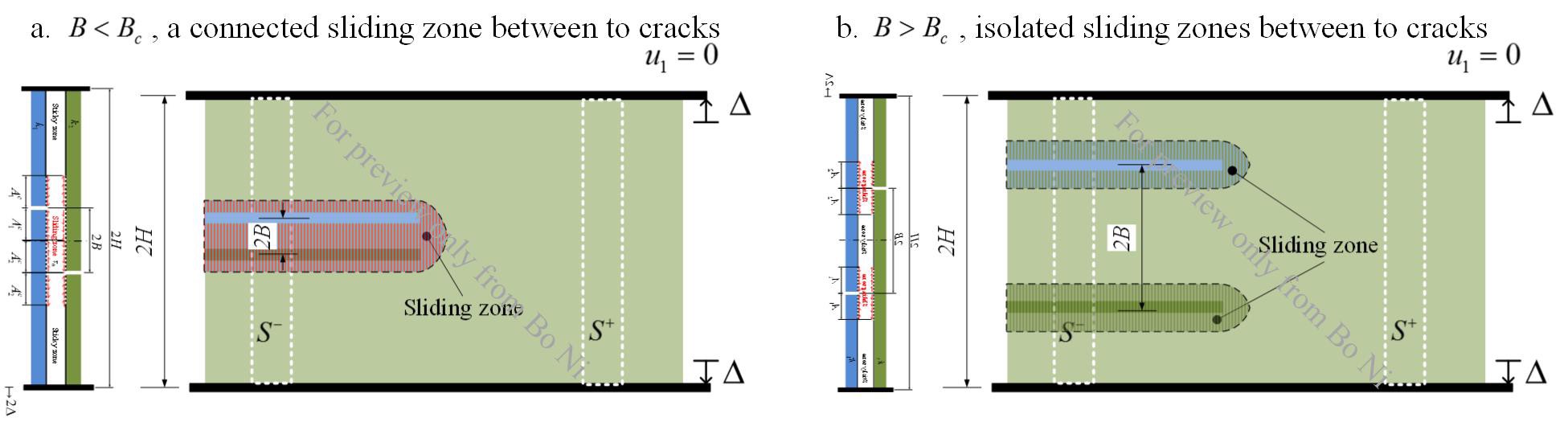
For cracks with dissimilar paths, we find there exist critical distance determined by the fracture and friction properties of the layers, beyond which the two cracks will not “feel” each other and can propogate independently (Figure 7). This critical crack spacing make it possible to propogate multiple cracks in multilayered system (See the video below), which is in contract of the leading crack shielding effect in a monolayer case.
Propogate two cracks beyond shielding effect.
More detailes and related discussion can be found in the following publication.
Ni B, Gao H. Harness the Power of Fracture: Controlled Fragmentation of Graphene via Substrate Necking. Matter. 2020 Mar 4;2(3):521-4.
Ni B, Gao H. Crack propogation in multilayered 2D materials in the presence of interlayer sliding. (Under working)